Galicia. Examen PAU resuelto de Matemáticas II. Junio 2014

OPCIÓN A

     2.    a)   Calcula el punto simétrico del punto    respecto  al plano

b)   Sea r la recta perpendicular al plano    y pasa por el punto  . Consideremos la recta  . Estudia la posición relativa de r y s. Calcula la

       ecuación del plano paralelo a s que contiene a r.

 

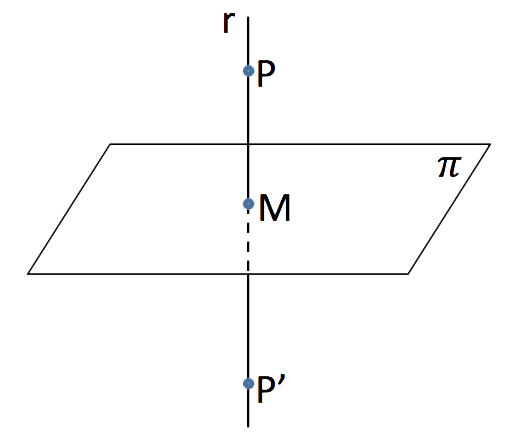
a)   Para  calcular  el  punto  simétrico,  primero,  vamos  a  calcular  la  ecuación  de la  recta  r  que  pasa  por  el  punto  P  y  es  perpendicular  al  plano  :

 

             

             

 

              

 

Ahora, calculamos el punto de corte de la recta r con el plano , es decir, el punto M. Para eso substituimos las ecuaciones paramétricas de la recta en la ecuación del plano, para obtener . Con ese valor de    vamos a las ecuaciones paramétricas de la recta y calculamos el punto:

Este punto, M, es el punto medio del punto P y de su simétrico, P’. Sabiendo esto ya podemos calcular el punto P’:

 

b)  El  vector  director  de  la  recta  r  va  a  se r el  vector  normal  del  plano,   puesto  que  es  perpendicular  a  este.  Como  además  sabemos  un  punto  de  la  misma  podemos  escribir  su  ecuación:

 

 

Por lo tanto sólo debemos estudiar la posición relativa de ambas rectas. Para eso primero calculamos un punto y el vector director de la recta s:

Si le damos a x = 0 :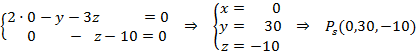  

 

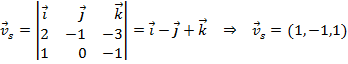
Para estudiar la posición relativa ,comparamosmos el rango de la matriz hecha con los vectores directores  y el de la matriz hecha con los vectores directores y con el vector que va desde un punto de una de las rectas a otro punto de la otra:

Estudiando el rango de estas dos matrices sabemos la posición relativa de las rectas:

Como el rango de A^* es 3 y el de A es 2, las rectas r y s se cruzan.

Para calcular la ecuación del plano que contiene a r y es paralelo a s, cogemos un punto de r y los vectores directores de las dos rectas, ya que uno está contenido en el plano que vamos a hacer y el otro es paralelo al mismo: