Galicia. Examen PAU resuelto de Matemáticas CC.SS.. Junio 2014

4.  En  un  reciente  estudio  se  afirma  que  hay  un 5% de lesiones de rodilla entre futbolistas que juegan sobre césped y calzan un nuevo modelo de botas de fútbol. De 250 futbolistas que juegan sobre césped y que calzan botas de fútbol convencionales se dieron 20 de tales lesiones.

(a)    Formula un test para contrastar la hipótesis de que la proporción de lesiones de rodilla jugando con botas convencionales no supera a las de tales lesiones jugando con el nuevo modelo, frente a la hipótesis de que sí la supera.

(b)   ¿A qué conclusión se llega con un 5% de nivel de significación? ¿Se llega a la misma conclusión con un 1% de nivel de significación?

(a)  Sea “p: proporción de lesiones de rodilla entre futbolistas que juegan sobre césped y calzan botas convencionales”.

: proporción muestral de lesiones de rodilla entre futbolistas que juegan sobre césped y calzan botas convencionales en muestras de 250 futbolistas.

Las hipótesis nula y alternativa son: 

(b)     Para un nivel de significación del 5%:

El estadístico de prueba sería: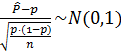 

Establecemos la región crítica: 

Evaluamos el estadístico de prueba, “bajo H₀ cierta”, para la muestra dada: 

Como     Rechazo H₀. Con los datos de esta muestra y con el  riesgo  de  equivocarnos  del  5%, concluiríamos que las lesiones de rodilla con botas convencionales supera a tales lesiones utilizando un nuevo modelo de botas (el último   riesgo   de   equivocarnos,   ante   esta   afirmación,   es   el  valor  de , es decir, de un 1,46%, siendo por lo tanto el test muy significativo).

Para un nivel de significación del 1%:

Establecemos la nueva región crítica: : 

Como     Acepto H₀. Con los datos de esta muestra y con el  riesgo  de  equivocarnos  del  1%, concluiríamos que las lesiones de rodilla con botas convencionales no supera a tales lesiones utilizando un nuevo modelo de botas.