Galicia. Examen PAU resuelto de Matemáticas CC.SS.. Septiembre 2014

2.    El beneficio B (en miles de euros) para una compañía que gasta una cantidad x (en miles de euros) en publicidad se estima por:  .

(a)      Calcula  la  cantidad  de  dinero que la compañía debe gastar en publicidad para que se produzca un beneficio máximo y calcula dicho beneficio. ¿Qué cantidad de dinero en publicidad le produce un beneficio mínimo?

(b)     Representa la gráfica de la función, utilizando los resultados anteriores y calculando concavidad, convexidad y punto de inflexión.

(a)   Para  calcular  los  máximos  y  mínimos  debemos  calcular  la  primera  derivada  de  la  función  e   igualarla a  cero:

Debemos ahora calcular la segunda derivada y substituir los puntos críticos en ella para saber si son máximos o mínimos:

Para calcular los beneficios máximos y mínimos substituimos estos valores y la inversión máxima en la función del principio:

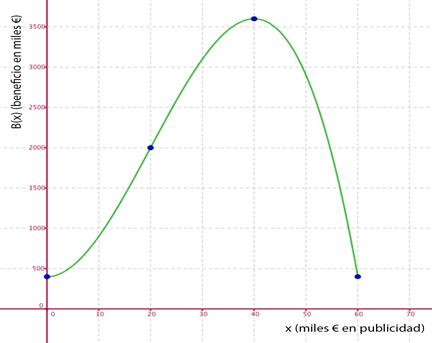
Para  un  gasto  de 40.000 € en publicidad, la empresa obtiene unos beneficios de 3.600.000 € y para un gasto de 0 € o de 60.000 € el beneficio que obtiene es mínimo.

(b)     Para calcular la curvatura igualamos la segunda derivada a cero:

El valor obtenido es un posible punto de inflexión. Con él y con el dominio de definición de la función, estudiamos la concavidad y la convexidad: 

Como en x = 20 cambia la curvatura, hay un punto de inflexión. Calculamos la otra coordenada del punto:

El punto de inflexión será el (20,2.000).

Con todos los datos calculados dibujamos la gráfica de la función: