Galicia. Examen PAU resuelto de Matemáticas CC.SS.. Junio 2014

2.   Los beneficios (en cientos de miles de euros anuales) estimados por una pequeña empresa durante un período de cuatro años, se ajustaron a la función  ,  , en donde B(x) representa los beneficios de la empresa a los x años transcurridos desde su constitución (x = 0 corresponde al año 2006).

(a)      ¿En algún año la empresa no tuvo beneficios? Justifica la respuesta.

(b)   Determina los intervalos de tiempo en los que los beneficios han aumentado y en los que han disminuido. ¿Qué información nos proporcionan sobre la evolución de los beneficios en esos cuatro años? Calcula los beneficios máximo y mínimo y los años en que se produjeron.

(c)    Utilizando los resultados anteriores y calculando, si lo hay, el punto de inflexión, representa la gráfica de B(x).

(a)      Para calcular si la empresa no tuvo beneficios, hacemos B(x) = 0:

Tenemos dos soluciones:

Sabemos, entonces, que no tuvo beneficios justo al arrancar la empresa y en el tercer año, es decir, en el 2009. Además también llegamos a la conclusión de que nunca tuvo pérdidas, porque la función beneficio, al x ser siempre un valor positivo, nunca va a ser menor que cero.

(b)   Para  ver  cuando  aumentan  y  cuando  disminuyen  los  beneficios,  estudiamos  el  crecimiento  y  decrecimiento de la función. Para ello:

Los valores obtenidos son posibles máximos o mínimos de la función beneficios. Con ellos y con el dominio de definición de la función, estudiamos el crecimiento y decrecimiento:

El primer año aumentaron los beneficios, del primer al tercer año disminuyeron y el último año volvieron a aumentar. Hay un máximo en el primer año y un mínimo en el tercer año. Vamos a calcular a cuanto ascendieron. Además vamos a calcular también los beneficios el último año, ya que estos aumentaron y pudiera ser que superaran los del primer año:

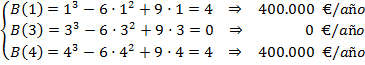
Los beneficios máximos se produjeron en el año 2007 y en el 2010 con 400.000 € anuales y los mínimos en el año 2009 con 0 € anuales.

(c)      Para calcular el punto de inflexión, hacemos la segunda derivada e igualamos a cero:

Para comprobar si es un punto de inflexión, lo substituimos en la tercera derivada:

   ⇒   x = 2 hay un punto de inflexión

   ⇒   Punto de inflexión en (2,2)

Con estos datos ya podemos hacer la gráfica: