Galicia. Examen PAU resuelto de Matemáticas II. Junio 2013

1.     

a)   Discute, según los valores del parámetro m, el siguiente sistema de ecuaciones lineales:

b)   Resuelve, si es posible, el sistema anterior para el caso de m=1.

a)   Planteamos las dos matrices asociadas al sistema, la de coeficientes y la ampliada:

      ;     

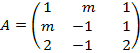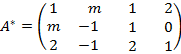
Ahora calculamos los rangos por determinantes:

   ⇒  

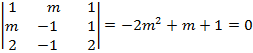−     Si    ⇒  rango (A) = 2   rango (A^*) = 3  ⇒  Sistema incompatible (sin solución).

      ;     

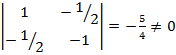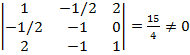
−     Si    ⇒  rango (A) = 2 = rango (A^*) < nº incógnitas ⇒  Sistema compatible indeterminado (infinitas soluciones).

   ;      ;      ;  

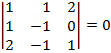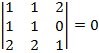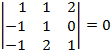
−     Si    y    ⇒  rango (A) = 3 = rango (A^*) = nº incógnitas  ⇒  Sistema compatible determinado (una solución).

b)   Según los cálculos hechos en el apartado anterior, si m=1 el sistema es compatible indeterminado.

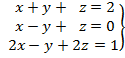
La primera ecuación es combinación lineal de la segunda y la tercera:  . Por lo tanto podemos eliminar esta ecuación y poner una incógnita como parámetro:

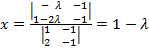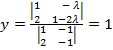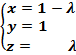    ⇒      ;      ⇒     λ