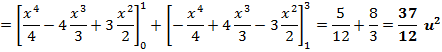Galicia. Examen PAU resuelto de Matemáticas II. Junio 2013

OPCIÓN A

 

4.     

a)   Calcula los intervalos de crecimiento y decrecimiento y los intervalos de concavidad y convexidad de la función  .

b)   Dibuja y calcula el área de la región limitada por la gráfica de    y la bisectriz del primer cuadrante. (Nota: para el dibujo de la gráfica de f(x), es suficiente utilizar el apartado anterior y calcular los puntos de corte con los ejes).

 

a)   El dominio de la función es , por ser una función polinómica. Para calcular los puntos críticos, hacemos  :

   ⇒      ⇒  

 

Mirando el signo que toma la primera derivada, en los intervalos resultantes y teniendo en cuenta que cuando dé positivo crece y cuando dé negativo decrece. Los intervalos quedan:

                  f(x) crece de

          f(x) decrece de         

 

Para estudiar la curvatura, hacemos   :

   ⇒      ⇒  

Miramos el signo que toma la segunda derivada en los  intervalos  resultantes.  Cuando  dé  positivo la función  es  convexa y cuando dé negativo cóncava:

               f(x) cóncava de

                   f(x) decrece de         

 

b)   Para dibujar la gráfica, calculamos los puntos de corte con los ejes:

 

Corte eje OX:  y=0

   ⇒      ⇒  Puntos de corte:    y 

 

Corte eje OY:  x=0

   ⇒      ⇒   Punto de corte : 

 

Con los datos del apartado anterior y los puntos de corte, se puede dibujar perfectamente la gráfica. Aprovechamos para pintar también la bisectriz del primer cuadrante, y=x :

 

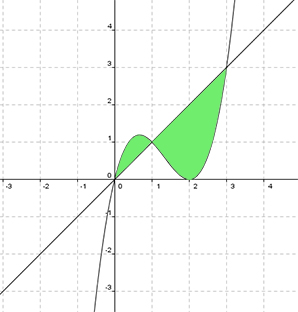
Debemos calcular los puntos de corte de la función y de la recta, para así poder calcular el área. Para ello resolvemos el sistema formado por las dos ecuaciones:

   ⇒     

 

Ahora podemos plantear las integrales, para calcular el área: