Galicia. Examen PAU resuelto de Matemáticas II. Junio 2013

2.    Dados el plano π:    y la recta  r:  .

a)   Estudia la posición relativa de r y π. Calcula la distancia de r a π.

b)   Calcula la ecuación general o implícita del plano que contiene a r y es perpendicular a π.

a)   Para calcular la posición relativa llega con calcular el rango de las dos siguientes matrices:

      ;     

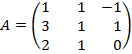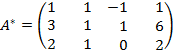
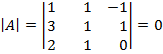   ⇒  rango (A) < 3. Como     ⇒   rango (A) = 2.

El rango (A^*) = 3, ya que: .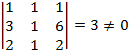

Por lo tanto, como rango (A) = 2  rango (A^*) = 3 ⇒  El plano y la recta son paralelos.

La distancia entre una recta y un plano paralelos, es la menor distancia de un punto cualquiera de la recta al plano. Por lo tanto, vamos a sacar un punto de la recta y para ello vamos a pasarla a las ecuaciones paramétricas:

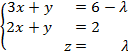   ⇒      ⇒   Resolviendo:  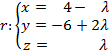   λ  

Entonces el vector y el punto de la recta r serían:  .

Ahora con este punto, , ya podemos calcular la distancia al plano:

b)   Como el plano que buscamos (σ) tiene que ser perpendicular al plano π, el vector normal de este plano está contenido en σ. También es un vector del plano que tenemos que hacer el vector director de la recta r (), ya que esta está contenida en el plano y lo mismo ocurre con cualquier punto de la recta, que también es del plano σ.

Por lo tanto, ya podemos determinar el plano que nos piden:

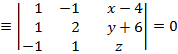σ   ⇒   σ