Galicia. Examen PAU resuelto de Matemáticas CC.SS.. Septiembre 2013

OPCIÓN A

 

2)   Sea la función .

(a)    Calcula a, b, c y d, sabiendo que la función presenta sus extremos relativos en los puntos    y 

(b)     Determina qué tipo de extremos relativos son cada uno de los puntos anteriores.

(c)    Representa la gráfica de la función, determinando los puntos de corte con los ejes y el punto de inflexión.

 

(a)  La condición que deben cumplir los extremos relativos es:  . Necesitamos entonces hacer la primera derivada de la función:

Ahora, aplicamos las dos condiciones antes mencionadas:

Substituyendo el valor de c obtenido en la segunda ecuación tendríamos:

Además si los puntos   y   son extremos, la función pasa por esos puntos, por lo tanto   y  . Aplicando estas dos nuevas condiciones obtenemos:

Substituyendo el valor de c y d, ya calculados, en esta segunda ecuación nos queda:

Para terminar, sólo resta resolver el sistema que resulta:

Los valores pedidos son:  .

 

(b)     Con los valores obtenidos en el apartado anterior, la función queda de la siguiente manera:

Ahora, hacemos las dos primeras derivadas:

Para saber si los extremos anteriores son máximos o mínimos los substituimos en la segunda derivada y decidimos en función del signo obtenido:

   En el punto (0,0) hay un mínimo relativo.

   En el punto (1,1) hay un máximo relativo.

 

(c)      Primero vamos a calcular los puntos de corte con los ejes:

Corte eje OX:

Corte eje OY:

Para calcular el punto de inflexión debemos igualar la segunda derivada, que ya teníamos calculada, a cero:

Para comprobar si en este punto realmente hay un punto de inflexión deberemos hacer la tercera derivada y substituirlo en la misma:

 punto de inflexión en

Ahora calculamos la otra coordenada del punto de inflexión:

El punto de inflexión es  .

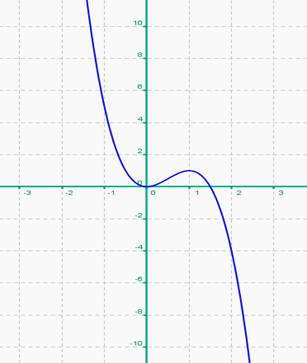
Con todo lo que tenemos calculado de la función, podemos directamente hacer una representación gráfica de la misma. Quedaría algo así: