Ejercicio resuelto de rango de matrices estudiando la dependencia lineal de sus filas
17. Determina el rango de las siguientes matrices:
.png)
Para la matriz A:
Vemos que ninguna de las filas es proporcional a otra, porque no podemos multiplicar ninguna de ellas por ningún número y obtener la otra. Veamos si alguna de ellas es combinación lineal de las otras dos:
.png)
Como los valores obtenidos de ![]() son iguales entre sí y los de
son iguales entre sí y los de ![]() también, la primera ecuación se puede poner como combinación lineal de las otras dos, por lo tanto el rango de la matriz no es 3, sino 2.
también, la primera ecuación se puede poner como combinación lineal de las otras dos, por lo tanto el rango de la matriz no es 3, sino 2.
.png)
Para la matriz B:
Como ![]() y
y ![]() , todas las filas son proporcionales. Por lo tanto el número de filas linealmente independientes es uno.
, todas las filas son proporcionales. Por lo tanto el número de filas linealmente independientes es uno.
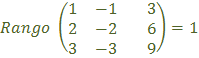
Ejercicio resuelto de rango de matrices estudiando la dependencia lineal de sus filas
Se calcula el rango de dos matrices comprobando si alguna de sus filas es combinación lineal de las otras

