Operaciones con vectores

1.      Dados los vectores ,  y :

a)  Halla los vectores    y  .

b)  Calcula a y b tales que .

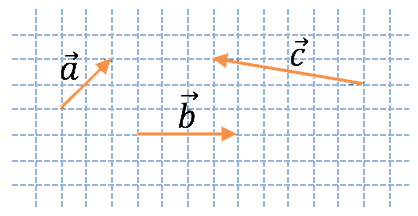
2.      Dados los vectores de la figura, dibuja los correspondientes a las siguientes operaciones:

a)                                                b)                                              c)

d)                                           e)                                  f)

3.      Sean los vectores , ,  y . Calcula  ,  y  para que se cumpla:

4.      Estudia  la  dependencia  lineal  de  los  siguientes  conjuntos  de  vectores,  dados  por  sus  coordenadas en una base B:

a)  .

b) 

5.      Determina el número máximo de vectores independientes, y elige los vectores que lo sean:

6.       

a)  Determina los valores de a para los que resulten linealmente dependientes los vectores ,  y .

b)  Obtén en esos casos una relación de dependencia entre los vectores.

7.      Comprueba si los vectores cuya expresión respecto de la base  es ,  y , son base del espacio.