Ley de gravitación universal

9.       Dos esferas de 200 kg se encuentran separadas 1 m a lo largo del eje OY. Halla la fuerza neta que ejercen sobre una pequeña masa de 0,1 kg situada sobre el eje OX a 0,25 m del punto medio de las esferas. Expresar el resultado en forma vectorial y calcula el módulo de la fuerza neta.

DATO: 

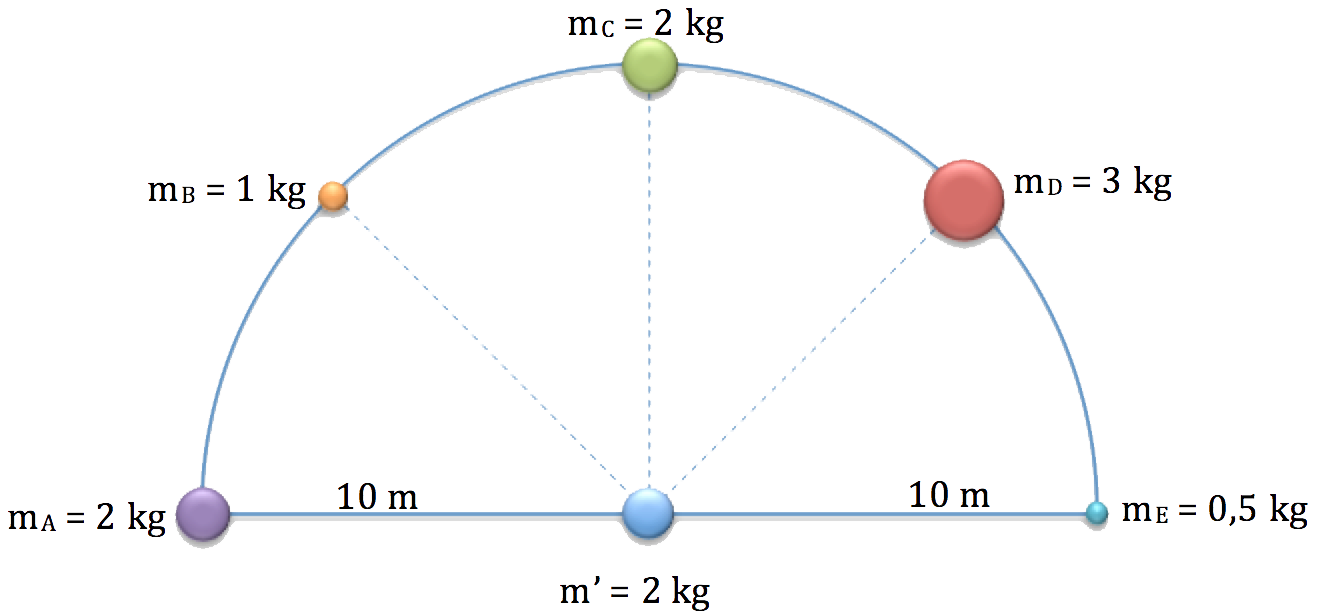
10.      Determina la fuerza que actúa sobre la masa m’ de la distribución que aparece en la siguiente figura:

11.      Explica el concepto de campo. Pon un ejemplo de campo escalar y otro de campo vectorial.

12.     Justifica si es cierta o no la siguiente afirmación: “Cuando dos masas M₁ y M₂ crean un campo gravitatorio en la misma región del espacio, hay puntos en los que se cruzan las líneas de campo que crea cada una de ellas y puntos en los que se cortan las superficies equipotenciales correspondientes a cada una de ellas”.

13.     Di qué propiedades cumplen los campos de fuerzas conservativos. ¿Qué magnitud se asocia a estos campos? Cita algunos ejemplos de campos conservativos.

14.    Explica qué utilidad tienen las líneas de campo y las superficies equipotenciales de un campo de fuerzas. ¿Dónde dibujaremos más juntas las líneas de campo, cerca de las masas o lejos de las mismas? Justifica las respuestas.

15.   Dos masas puntuales de 2 kg están situadas en los extremos de la hipotenusa de un triángulo rectángulo isósceles con catetos que miden 3 m. Calcula:

a)    El módulo del campo gravitacional en el tercer vértice del triángulo.

b)   El módulo de la fuerza gravitacional que actúa sobre una masa de 10 g colocada en ese punto.

16.     Tres masas puntuales de 10³ kg cada una, están fijas en los vértices de un triángulo equilátero de 1 m de lado. Calcula:

a)    La fuerza que actúa sobre una cualquiera de ellas.

b)   Si se deja en libertad una de las masas, ¿qué velocidad tendrá cuando pase por el punto medio de las otras dos?

DATO: 

17.   Dos masas iguales puntuales de 5 kg se encuentran situadas en los vértices inferiores de un triángulo equilátero de 40 cm de lado. Si se coloca en el vértice superior una masa m’:

a)    ¿Qué aceleración adquiere esa masa en ese punto? Expresa el resultado en forma de vector.

b)   ¿Descenderá con aceleración constante?

c)    ¿Qué aceleración tendrá en el momento de llegar a la base del triángulo?

DATO: